Luminescence, optics and magneto-optics software (LOMS)

Online tool for data fitting, simulation and evaluation

    • MODULE: Judd-Ofelt analysis and Combinatorial Judd-Ofelt analysis

    Important instructions:

    • Complete and detailed description of this module is presented in:” J.Hrabovsky, P. Varak, R. Krystufek, LOMS: interactive online software for Classical and Combinatorial Judd-Ofelt analysis with integrated database of Judd-Ofelt parameters, preprint, 8. August 2024″ (free download) and works published using this LOMS online tool shall reference this article.
    • LOMS.cz: Judd-ofelt module is freely accessible at www.loms.cz/jo and the LOMS.cz: Judd-Ofelt parameters database is available under link www.loms.cz/jo-database
    • Complete set of reference files and templates is placed at the end of this documentation
    • Please refer feedback and error bugs via Contact form or use email box: info@loms.cz

    Sections:

    1. Judd-Ofelt theory
    2. Judd-Ofelt theory: Experimental practice
    3. Combinatorial Judd-Ofelt analysis
    4. LOMS: Graphical user interface
    5. Data records, templates, references, imports and output files
    6. Templates & Reference files
    7. References

     

     

    1. Judd-Ofelt theory

    JO theory was introduced independently to each other by Brian R. Judd [1]  and George S. Ofelt [2] in 1962 based on the previous work of J.H. Van Vleck about spectroscopic properties of rare-earth ions in solids [3]. Sharp spectroscopic lines of RE3+ ion implicated the intra-4f electronic transitions that occur between the levels inside the 4f electronic shell. This is, however, forbidden by the Laporte selection rule which says that states with even parity can be connected by electric dipole transitions only with states of odd parity and the same in vice versa. Among the other proposed but incorrect explanations based on (1) 4f to 5d transitions or (2) magnetic dipole or electric quadrupole radiation, Van Vleck [3] and Broer [4] presented a reasonable solution based on the distortion of the electronic motion by surrounding crystal/ligand field in the material. Presented distortions then bypass the Laporte selection rule and allow the electric dipole radiation even for intra-4f electronic transitions. However, to disturb the wavefunctions and negate the Laporte rule, the external field must also be noncentrosymmetric. From this point, about a quarter of a decade later and with further advances in algebra, computing, and increased applications of lasers, JO theory[1,2] was presented and described the induced electric dipole transitions of RE3+ ions in host materials. JO theory then provides a theoretical expression for the calculation of oscillator strengths (Eq. 1), as the ratio between absorbed (emitted) and emitted (absorbed) intensity of electromagnetic radiation for harmonically oscillating electron and expresses the probability of individual J↔J’ transition as follows,

    (1)   \begin{equation*}f\textsubscript{theor}(J \rightarrow J')= \frac{8\pi\textsuperscript{2}m\textsubscript{e}c}{3h\overline\lambda (2J+1)} n\left(\frac{n\textsuperscript{2}+2}{3n}\right)^2 \sum_{i=2,4,6} \Omega_i | \langle (S,L)J | U^i | J'(S',L') \rangle |\textsuperscript{2},\end{equation*}

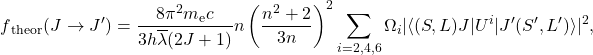
    where J and J′ are the quantum numbers of the initial ground state and excited state, respectively, n is the refractive index, h is the Planck’s constant, me is electron mass, c is the speed of light in vacuum, λ is the mean wavelength of corresponding J→J’ transition and Ωi are the JO parameters for i = 2, 4, 6. The terms in brackets are the squared reduced matrix elements, which are almost independent on the host matrix. Note, that the summation over i is also known as manifold linestrength which will be introduced later in this section. Interaction between the surrounding host matrix and RE3+ ions are then expressed by the set of three JO phenomenological parameters, which can be obtained by equating the expressions for the experimental ( fexp) and theoretical ( ftheor) oscillator strengths using the least-squares method. The experimental oscillator strengths can be calculated from optical absorption spectra using the Eq.2

    (2)   \begin{equation*}f\textsubscript{exp}(J \rightarrow J')= \frac{2m\textsubscript{e}c}{\alpha_f h \overline\lambda^2 N} \int \alpha (\lambda)d\lambda,\end{equation*}

    where αf is fine structure constant, N is rare-earth ion concentration and α(λ ) is wavelength-dependent absorption coefficient. Optical absorption can be also expressed using the absorption cross section, σ abs, defined as σ abs = α(λ )/N. Using knowledge of the JO parameters, several important spectroscopic quantities can be calculated for a specific material system, such as the transition probabilities, A(J′, J), radiative lifetimes, τJOr, or the luminescence branching ratios, β (J′, J). The transition probabilities for each transition are calculated from Eq. 3:

    (3)   \begin{equation*}A(J'\rightarrow J)= \frac{64\pi\textsuperscript{4}e^2}{3h\lambda_B^3 (2J'+1)} \left( \chi\textsubscript{ED} S\textsubscript{ED} + \chi\textsubscript{MD}S\textsubscript{MD} \right) ,\end{equation*}

     

    where J′ is the total angular momentum of the upper excited state, λB is the transition wavelength (also called Barycenter), SED and SMD are electric and magnetic dipole line strengths and χED and χMD are the local field corrections of the electric dipole (Eq.4) and the local field correction of the magnetic dipole (Eq.5)

    (4)   \begin{equation*}\chi\textsubscript{ED}=n\left( \frac{n\textsuperscript{2}+2}{3} \right)^2 ,\end{equation*}

    (5)   \begin{equation*}\chi\textsubscript{MD}=n^3 ,\end{equation*}

    The electric dipole linestrength is then easily calculated from each excited state manifold to lower lying manifold using the JO parameters and matrix elements by Eq. 6:

    (6)   \begin{equation*}S\textsubscript{ED}= \sum_{i=2,4,6} \Omega_i | \langle (S,L)J | U^i | J'(S',L') \rangle |\textsuperscript{2},\end{equation*}

    where $e$ is unit charge of electron. The magnetic dipole line strengths are given by Eq. 7:

    (7)   \begin{equation*}S\textsubscript{MD}=\left( \frac{h}{4 \pi m\textsubscript{e}c} \right)^2 | \langle (S,L)J | \hat{L}+g\hat{S} | J'(S',L') \rangle |\textsuperscript{2},\end{equation*}

    where g is the electron g-factor (g≈ 2.002 ) and the terms in brackets are reduced matrix elements of the |L + gS| operator. The radiative lifetimes of each level, τJOr, are then calculated from the transition probabilities using Eq.8. The luminescence branching ratio, β (J′, J) is given by Eq.9 and represents the distribution of the emission transitions in the emission spectra. Combining the theoretical JO lifetime and branching ratio with the experimentally measured lifetime, τr, for a designated transition results in Eq.10, which defines the radiative quantum yield, η, of the corresponding J′ → J electronic transition.

    (8)   \begin{equation*}\tau\textsuperscript{JO} \textsubscript{r}= \frac{1}{\sum_{J'}A(J',J)},\end{equation*}

    (9)   \begin{equation*}\beta (J',J)= \frac{A (J',J)}{\sum_{J'}A(J',J)},\end{equation*}

    (10)   \begin{equation*}\eta (J',J)= \frac{\tau\textsubscript{r}}{\tau\textsuperscript{JO}\textsubscript{r}}\beta(J',J),\end{equation*}

    The quality of the least-squares fit can be quantified by the σ RMS parameter, expressed by Eq. 11

    (11)   \begin{equation*}\sigma \textsubscript{rms}= \sqrt{\frac{\sum (f\textsubscript{exp}-f\textsubscript{theor.})^2}{T-3}} ,\end{equation*}

    where T is the number of transitions used for the calculation.

     

    2. Judd-Ofelt theory: Experimental practice

    From the experimental perspective, accurate spectroscopic characterization of the prepared materials is essential for the proper application of the JO theory and estimation of JO parameters, transition probabilities and derived values of branching ratios and theoretical luminescence lifetimes.  


    The first step of the JO analysis requires the measurement of the transmission spectrum, T (λ ), to determine the wavelength dependent values of the absorption coefficient, α(λ ), and then the values of the absorption cross-section, σabs(λ ) . Although the calculation of the σabs(λ ) value from the absorption coefficient using the known RE3+ ion concentration (N) is relatively simple, where σabs(λ ) = αk(λ )/N, the calculation of the absorption coefficient may vary across the literature depending on whether scattering losses are not included (12), included (13) and if taking into account multiple reflections in plane parallel geometry of the sample (14) (in the case of solids). As is visible from Fig.1 in the example of RE3+-doped glass, the spectral shape of corresponding transitions in the transparent region is practically identical with significant offset caused by the not included/included reflectivity (R). In cases where the absorption band is offset from the zero σabs(λ )  value or overlaps with the absorption edge, it is therefore necessary to subtract the background to obtain the most possible accurate value. If the number of observed manifolds is sufficient, it is recommended to exclude the transitions within the absorption edge from the calculation of the JO parameters to increase fit accuracy.

    (12)   \begin{equation*}\alpha\textsubscript{1} = \frac{-1}{l}ln(T) = \frac{-2.303log\textsubscript{10}(T)}{l}\end{equation*}

    (13)   \begin{equation*}\alpha\textsubscript{2} = \frac{-1}{l} ln \left(\frac{T}{(1-R)^2} \right)=\frac{ 2.303\left[-log\textsubscript{10}(T)+log\textsubscript{10}(1-R)^2\right]}{l} \end{equation*}

    (14)   \begin{equation*}\alpha\textsubscript{3} = \frac{1}{l}ln \left[ \frac{ (1-R)\textsuperscript{2}+\sqrt{(1-R)\textsuperscript{4}+4R^2T^2}}{2T} \right]\end{equation*}

     

    Derived spectral dependence of the σ abs(λ ) is used for estimation of the integrated absorption cross section, ∫ σabs(λ )dλ (in cm2 nm), for each manifold (Fig.1b) which is then used for calculation of the experimental oscillator strength (Eq.2) or experimental linestrength (Eq.15) according to

     

    (15)   \begin{equation*}S\textsubscript{exp}(J \rightarrow J')= \frac{3ch(2J+1)}{8\pi^3e^2\overline\lambda}n\left(\frac{3}{n^2+2} \right)^2\int_{J\rightarrow J'} \sigma (\lambda)d\lambda,\end{equation*}

    where J is the quantum number representing the total angular momentum of the original ground state, found from the 2s+1LJ term constructed by using the three Hund’s rules (see previous section for detailed description). As the linestrength is typically referred in cm2, the units and input values for other quantities and constants in presented calculations are used as follows: speed of light, c = 3 × 1010cm s-1, Planck constant, h = 6.626 × 10-30 cm2 kg -1s, unit charge of electron, e = 1.5189 × 10-11 cm3/2 kg1/2 s-1, fine structure constant, α = 7.297 × 10-3 ≈ 1/137 , and electron mass, me = 9.11 × 10-11kg. The last presented parameter, mean wavelength, can be found as well from the absorption cross section data using the harmonic, λH (Eq.17a), or weighted mean value, λW (Eq.16b), for each transition as is illustrated in Fig.1b. Both derived mean values lead to almost similar results, which, however, may differ from the value of simply subtracting absorption band maximum, λmax. Note, that for the proper calculation of experimental oscillator strength or experimental linestrength, the values of experimentally determined integrated cross section and mean wavelength must be recalculated after subtraction from the graph and used in (cm2 cm) and (cm), respectively.

     

    (16)   \begin{equation*}\text{(a) }\overline\lambda\textsubscript{H} = \frac{1}{\frac{\sum\lambda\sigma\textsubscript{abs}(\lambda)}{\sum\sigma\textsubscript{abs}(\lambda)}}=\frac{\sum\sigma\textsubscript{abs}(\lambda)}{\sum\lambda\sigma\textsubscript{abs}(\lambda)} \text{ or } \text{(b) } \overline\lambda\textsubscript{W} = \frac{\sum\sigma\textsubscript{abs}(\lambda)\lambda}{\sum\sigma\textsubscript{abs}(\lambda)}\end{equation*}

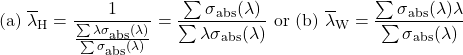
    By completing all of the above characteristics, the JO phenomenological parameters, Ωi(i = 2, 4, 6) are determined by fitting the experimental absorption represented by experimental oscillator strength (Eq.2) or linestrength (Eq.15) using the least square method to the theoretical ones described via Eq.(1) or Eq.(6). On the example of the second case, experimental and theoretical linestrengths are written in their respective matrix forms similarly as described in Ref.[5] and the sum of the square difference is minimized. Since the JO theory includes only three parameters, more than three absorption manifolds have to be provided for calculation, and thus JO theory cannot be applied to single Yb3+-doped materials. After fitting procedure, materials characteristics, such as A(J′,J), β (J′, J) and τJOr, are calculated using the known JO parameters from Eq.3, Eq.8 and Eq.9. Nevertheless, for proper calculation of transition probabilities (Eq.3), it is also necessary to know the value of corresponding transition (J′ → J) wavelength from an excited state to the ground/lower-energy state, λB, also commonly referred as Barycenter. This value should be in principle different from the mean wavelength λ or absorption band maximum (λmax). However, the assignment of the barycenter varies considerably within the literature (or is not clearly explained) and can be divided into three main approaches, using the (1) similar value of mean wavelength λ derived from the optical absorption measurements as Barycenter or (2) tabulated values assigned with U2,U4,U6 elements regardless of the host material or (3) the peak/mean wavelength derived from emission spectra at room temperature. Using the last approach, it is possible to estimate the spectral shift between mean absorption and emission wavelength for one transition and then apply this difference to all other transitions. Given the extensive nature of the topic, it is up to the author which approach is chosen and which would best fit the experimental results.

     

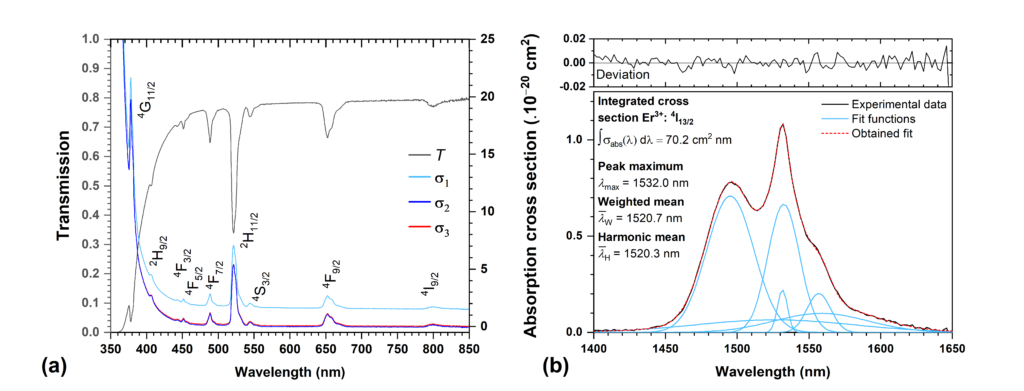
    Fig.1. (a) Transmission spectrum and corresponding absorption cross sections, employing various corrections on scattering losses or plane parallel geometry of the sample; (b) example of integrated area calculation of a selected band

     

    3. Combinatorial Judd-Ofelt analysis


    Following the previous section, it is clear that the selection of the appropriate transition bands and their experimental description is crucial for accurate calculation of the JO parameters[5-7]. To compute the JO parameters, at least four experimentally measured absorption manifolds must be used. When a larger set of measured absorption bands is available, it becomes possible to exclude certain transitions (e.g., those exhibiting hypersensitivity) or to limit the JO analysis to transitions within a specific spectral region, for example, due to experimental limitations or the presence of fundamental absorption of the host matrix. However, for accurate determination of the complete set of all three JO parameters, the following criteria must be met: (1) the involved transitions must have non-zero values of the corresponding reduced squared matrix elements Ui (i = 2, 4, 6), (2) these values should be of the same order of magnitude, and (3) at least three transitions that satisfy the previous two conditions must be used. As a result, various studies exclude hypersensitive transitions, such as the 2H11/2 transition for Er3+ ions with a high U2 value, do not cover the full spectral range due to the lack of experimental capability to measure absorption bands in the NIR/MIR regions (Nd3+ (4I11/2), Dy3+ (6H13/2), Sm3+ (6H7/2 and 6H9/2), etc.) or selectively include/exclude transitions affected by the absorption edge. This last scenario can be particularly limiting for materials with low optical transmission in the visible spectral region, such as chalcogenide glasses, since this region typically contains the majority of experimentally observable absorption bands associated with rare-earth ions. For some materials, it is therefore in principle necessary to include the transitions affected by the absorption edge, otherwise they would not meet the condition for the minimum number of used manifolds. Using Combinatorial Judd-Ofelt analysis (C-JO)[7] and a higher than minimum number of transitions, it is thus possible to identify those manifold combinations that enable accurate JO analysis ensuring consistent and reliable results. Moreover, by employing various types of host materials and broad-spectrum analysis for each eare-earth ion it will be possible to identify such critical combinations, which are essential for the calculation of JO parameters and thus should not be omitted.
    The total value of all possible combinations then depends on the number of input absorption bands (NB) according to Eq.17

     

    (17)   \begin{equation*}\text{Total combinations} = \sum_{r=k}^{N\textsubscript{B}} \binom{N\textsubscript{B}}{r} \end{equation*},

     

    where k is the minimum number of elements in each combination (from 4 to NB) and (NB/r) is the binomial coefficient calculated as (NB/r) = NB!/(r!(NB−r)!). It is then possible to obtain 5, 22, 64, 163, 382 and 848 possible combinations for original sets composed of 5, 6, 7, 8, 9 and 10 experimentally obtained absorption bands. The obtained set of all possible combinations can be subsequently reduced by inappropriate combinations using different empirical approaches (e.g. due to unphysicality of partial solutions or non-converging results when calculating JO parameters) or using the analysis of statistical distribution of the resulting JO parameter values depending on the absorption bands used[7]. In order to eliminate the empirical selection approach, the box/whisker plot statistical method may be applied to the original set of all possible combinations reduced by the non-physical cases (negative values of JO parameters)[7]. According to the used statistical model, data points (combinations) outside the whisker boundaries are identified as outliers and thus may be excluded from the dataset as was shown in Ref.[7] on the example of Er3+-doped materials. Several other examples of presented C-JO analysis are given in the following sections or in the main manuscript body of reference article.
     

     

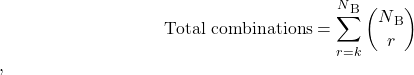
    schema_programu

    Fig.2. Software procedure of Judd-Ofelt analysis and implementation of Judd-Ofelt parameters database.

    4. LOMS: Graphical user interface

    The process of JO and Combinatorial JO analysis using the Luminescence, optics and magneto-optics software (LOMS) (www.LOMS.cz) is captured in the attached flowchart (Fig.2) and the GUI of LOMS software is shown in Fig.3. To enhance versatility, users can select from four recommended input options based on the desired level of data processing/verification (Fig.3, Radio button: Input values). The capability for direct processing of experimental oscillator strength/linestrength input data was implemented to facilitate potential comparison with experimental data in the literature. Furthermore, the possibility of direct input of JO parameters and subsequent calculation of material radiative characteristics has been added. The list of possible input files is as follows:

    1. Integrated absorption cross section ∫ σabsdλ (in cm2 nm) or
    2. Experimental oscillator strength, fexp, taken from an external source or calculated using Eq.2 or
    3. Experimental linestrength, Sexp (in cm2), taken from an external source or calculated using Eq.15 or
    4. Judd-Ofelt parameters, Ω2, Ω4, Ω6, (in cm2), taken from an external source or calculated using aforementioned procedure.

    Furthermore, to successfully calculate JO parameters and radiation material characteristics (transition probabilities, radiative lifetimes and branching ratios), the input file must be supplemented with the following data sets for each experimentally derived manifold:

    1. Refractive index (Fig.3, Radio button: Refractive index values) and
    2. Mean peak wavelength (in nm) derived using Eq.17 for each placed transition (Fig.3, Text field: Mean peak wavelength)
    3. Square matrix elements U2, U4, U6 for each placed transition (Fig.3, Text fields: U2, U4, U6)
    4. Barycenter: (in cm-1) for each transition. If they are not experimentally detectable, it is necessary to use their tabulated values or choose one of the approaches discussed further in this section (Fig.3, Text fields: Barycenter).

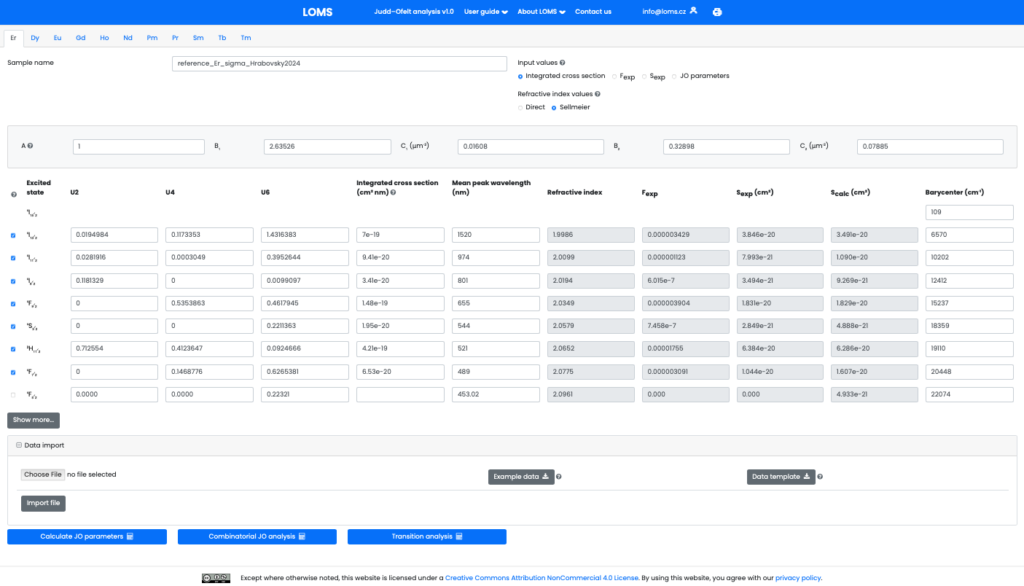
    Fig.3. The graphical user interface of LOMS online tool, which is available at https://www.LOMS.cz/.

    The refractive index can be added directly as defined values for each transition in the same row (Fig.3, Text field: Refractive index) or expressed using a standard two-term Sellmeir model (Eq.18)

    (18)   \begin{equation*}n\textsuperscript{2} = A+ \frac{ B\textsubscript{1}\lambda\textsuperscript{2}}{\lambda\textsuperscript{2}-C\textsubscript{1}} + \frac{ B\textsubscript{2}\lambda\textsuperscript{2}}{\lambda\textsuperscript{2}-C\textsubscript{2}},\end{equation*}

    where the A, B1, C1, B2 and C2 are the Sellmeier coefficients. Note, that while it is possible to directly enter the refractive index values (sufficient for calculation of JO parameters), calculating the radiation characteristics, A(J′, J), β (J′, J) and τJOr, requires inputting its spectral dependence via the specified Sellmeier coefficients. If the refractive index of the material is not directly available, it can be obtained from one of the accessible material databases, such as refractiveindex.info. A consistent set of tabulated matrix elements for all RE elements and default values of barycenters and mean peak wavelengths are provided (see Figshare repository[8] or www.LOMS.cz) with the possibility of their interactive editing in the software GUI if necessary. An important added functionality is also the possibility to interactively select the number of involved transitions (column of checkboxes on the left side in Fig.3) without the need to change/modify the input data structure. Once all the above requirements have been met, the classical JO analysis can be calculated via pressing button Calculate JO parameters and complete combinatorial JO analysis for all possible combinations of inserted absorption bands can be performed by pressing the Combinatorial JO analysis. The results structure in GUI is shown in Fig.4.

    loms_gui

    Fig.4. The graphical user interface of LOMS online tool (https://www.LOMS.cz.): Illustrative example of results structure for classical and combinatorial Judd-Ofelt analysis

    Note, that in many cases, two or more closely located transitions may overlap with each other and therefore it is not possible to easily distinguish their independent contribution. This can be the example of two absorption bands 2H11/2 (≈ 530 nm) and 4S3/2 (≈ 550 nm) in Er3+-doped materials. In such cases, it is therefore necessary to apply a modified procedure for the calculation of JO parameters as follows: (1) estimate the combined integrated absorption cross section which involves both absorption bands, (2) estimate the mean peak wavelength in the same way as if it was a single absorption band, (3) sum the respective matrix elements of all the participating transitions into one and (4) write them to the LOMS.cz online GUI in one line – choose the line of one of the involved transitions (or similarly in input .csv file). This modified procedure then affects the U2, U4, U6, integrated cross section and mean wavelength cells. For better clarity, the difference is visible in Fig.(5) and the data repository[8] also contains two .xls reference files with the shown calculation process (or is possible to download them HERE). It is also important to note, that it is necessary to uncheck the remaining transitions so that only the one combined transition/row participates in the calculation. This then acts as the combined level of 2H11/2 +4S3/2. It is then necessary to remember that in the output file of the JO analysis and the combinatorial JO analysis, this transition no longer represents only one level, but combination of all involved manifolds. However, this no longer applies to the calculation of radiative transitions properties (A, β , τ), which is done separately and independently of whether the combined or single bands were used for the calculation of JO parameters or not. This is of course due to the fact that radiative properties are calculated directly from the JO parameters, i.e. energy level assignment in Transition analysis section is independent of the structure of the data input.

     

    loms_gui4_multibands

    Fig.5 The graphical user interface of LOMS online tool, with shown comparison between data input structure without and with observed absorption band overlap. See the main text for discussion.

     

    Table 1. Calculated Judd-Ofelt radiative transition properties in TZB:Er glass using LOMS.cz online tool (in similar format as the software output file). The Transition eState represent the initial excited state (J′), Transition gState represent the final ground/lower lying state (J), λem is the emission wavelength calculated as the difference between involved energy levels which positions is represented by insterted values of Barycenters, S(ED) and S(MD) are electric and magnetic dipole line strengths and their respective contributions to the electric and magnetic transition probabilities A(ED) and A(MD), β is the branching ration and last two columns represent the calculated values of radiative lifetime using the LOMS.cz online tool and those taken from Ref.7.

     

     

     

     

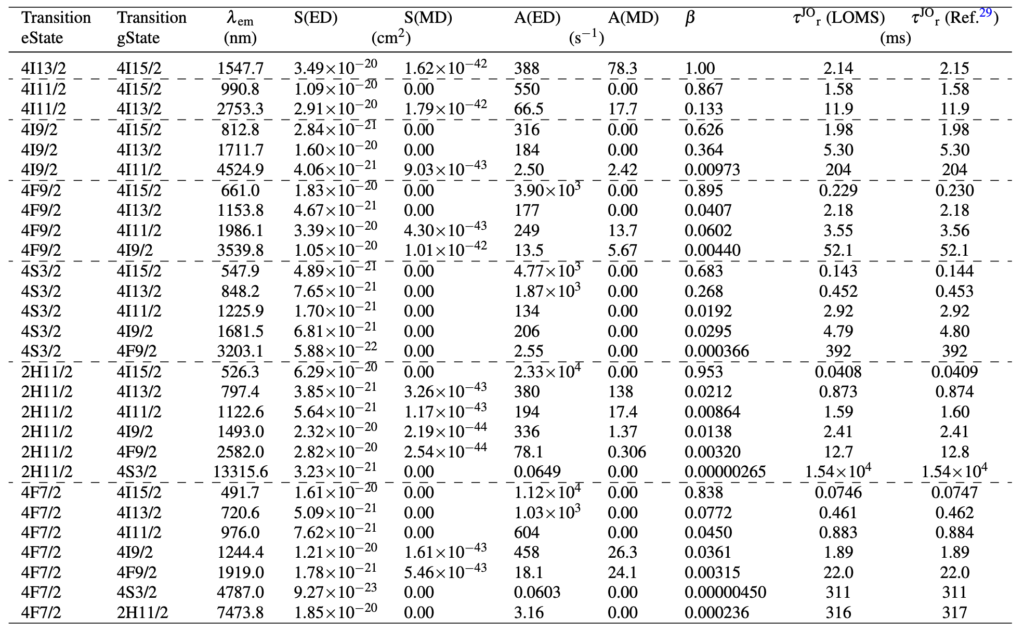
    Results of transition analysis, calculation of A(J′, J), β (J′, J), τJOr, A(ED), A(MD), will be displayed after pressing the Transition analysis button (see Fig.3). The results structure for radiative transition analysis in GUI is shown in Fig.6 and the structure of example output file is visible from Table1. Note, that for successful transition analysis, it is also necessary to include the Barycenter values for each transition and not only for those which were inserted. It is because the transition probabilities, A(J′, J) (Eq.4), are calculated for each transition (J′ →J) from an excited state to the ground/lower-energy state. As was discussed in the section Judd-Ofelt theory: Experimental practice, the barycenter value should be in principle different from the mean wavelength λ or absorption band maximum (λmax) as the position of photoluminescence emission is usually red-shifted compared to position of optical absorption (this is valid for both peak/mean wavelength values). However, the assignment of the barycenter varies considerably within the literature (or is not clearly explained) and can be divided into three main approaches, using the (1) similar value of mean wavelength λ derived from the optical absorption measurements as Barycenter or (2) tabulated values assigned with U2, U4, U6 elements regardless of the host material or (3) the peak/mean wavelength derived from emission spectra at room temperature. To avoid limiting of the calculation, the software allows all the above-mentioned options depending on the selected value. The LOMS.cz software then calculates the energy difference between selected energy levels, which will be used for the calculation of transition probabilities (Eq.3). The barycenter values may be then inserted as follows:

    1. Barycenter value similar to mean wavelength: (1) leave the first box for the ground state in Barycenter column (Fig.3, Text fields: Barycenter) blank or equal to zero, (2) fill the other positions with corresponding recalculated values of mean wavelength in cm-1 (cm-1 = 107/nm)
    2. Tabulated values of Barycenter: fill the corresponding manifold cell for each transition using the tabulated values
    3. Barycenter value with the constant shift: according to software procedure (JOFwin2011) presented by Walsh [5] possible to insert the offset position of the ground state which more or less represents the energy spectral shift between optical absorption and emission band peak/mean maximum. In this case, the value in the first box for the ground state in Barycenter column contains the value of this energy spectral shift, whereas the other values represents the mean wavelengths (in cm-1) derived from optical absorption spectra.

    Using the last approach, it is possible to estimate the spectral shift between mean absorption and emission wavelength for one transition and then apply this difference to all other transitions. Given the extensive nature of the topic, it is up to the author which approach is chosen and which would best fit the experimental results.

     

    loms_gui2

    Fig.6 The graphical user interface of LOMS online tool (https://www.LOMS.cz.): Illustrative example of results structure for Transition analysis

     

    5. Data records, templates, references, imports and output files

    The complete set of blank template input files for each rare-earth ion, illustrative examples of input files together with attached results for JO and C-JO analysis and dataset of JO parameters listed in LOMS.cz database is available at Figshare[8] or the www.LOMS.cz webpage (below this text or here).It presently, as of August 2024, contains:

    1. Template files: complete set of eleven templates for Pr3+, Nd3+, Pm3+, Sm3+, Eu3+, Gd3+, Tb3+, Dy3+, Ho3+, Er3+ and Tm3+ trivalent rare-earth ions which contains: identification of J → J′ transition with associated values of reduced matrix elements, mean-wavelenghts and barycenters obtained from Walsh[5] JOFwin2011 documentation as a reference. Templates are placed below this text.
    2. Reference files: example set of reference files with different types (I.−IV. of inputs, Fig.2) for JO analysis, C-JO analysis and calculation of radiative properties of Pr3+, Nd3+, Pm3+, Sm3+, Tb3+, Dy3+, Ho3+, Er3+ and Tm3+ trivalent rare-earth ions. Reference files and output files are placed below this text.
    3. Combinatorial Judd-Ofelt analysis: output files from C-JO analysis for RE3+-doped materials which contains JO parameters of all possible combinations of involved measured intre-4f transitions. Reference files and output files are placed.
    4. Database of Judd-Ofelt parameters: 1228 data records of JO parameters and resulting radiative properties for 12 RE3+ ions on 585 materials/host matrices of various compositions. The database is accessible via this website or can be read/downloaded from Figshare[8] data repository of public online Googlesheet.

    Structure of .csv file import


    To standardize and simplify the data upload process, users can utilize the option to upload the required data via a .csv file, using the provided templates for all elements. The template .csv file for each RE3+ ion is unique and cannot be exchanged between each other since it contains the corresponding absorption transitions notation, assigned square matrix elements, etc. To successfully complete the form, the following steps must be completed:

    1. Template file: Download the template file on the relevant rare-earth ion page (www.LOMS.cz/jo) or module documentation – at the end of this page (www.loms.cz/modules/judd-ofelt-analysis/) or from Figshare data repository[8]
    2. Refractive index import: Enter the refractive index input structure in the appropriate field following the ref_index_type cell (see Fig.7) as (1) sellmeier for input via Eq.18 or (2) direct for direct refractive index input. Based on your selection, enter either the Sellmeier coefficients or refractive index values for the corresponding transitions in the column labelled “refractive_index.”
    3. Transitions and Square matrix elements: verify/replace the tabulated square matrix elements but do not change the labels of the individual transitions in the first column.
    4. Input type: Select the corresponding form of your input type as follows: absorption cross section (sigma), experimental oscillator strength (fext), experimental linestrength (sexp) or JO parameters (jo) and write it down to the cell named input_date (rewrite it). The input values for corresponding transitions have to be placed in the same column. For the selection of JO parameters as an input (only for calculation of radiative properties), please insert the Ω2, Ω4, Ω6 JO parameters to the U2,U4,U6 of the ground state (replace the zero values).
    5. Mean peak wavelength: Enter the mean peak wavelengths for the transitions for which input data has been provided (see the previous text for proper estimation of mean wavelength value).
    6. Barycenter: Check or provide relevant data for all transitions, otherwise it will not be possible to calculate the relevant radiation characteristics. Please see Graphical user interface section for more details regarding the proper barycenter selection.
    loms_gui3_import_exp

    Fig.7 The structure of import .csv file.

    Structure of .csv output file


    Calculated results of JO analysis, Combinatorial JO analysis and radiative transition properties can be exported in the form of .csv files upon clicking on the button Export report in the corresponding section (see Fig.4 and Fig.6). Example output files for the mentioned references are included below this text and in Figshare repository[8] and correspond to the data structrures presented in Fig.4 and Fig.6. Data export from classical JO analysis also contains all input information for selected bands and both experimental and theoretical values of linestrength accompanied by the estimated ratios between calculated JO parameters

    6. Templates & Reference files

    Blank template: Er template

    Reference files:  
    1) Hrabovsky (2024) - 80TeO2-5ZnO-15BaO:Er (download all files) 2) Strizik (2014) - Ge25Ga9.5Sb0.5S65:0.5 at.%Er (download all files)
    Blank template: Dy template

    Reference files:  
    1) Cavalli (2002) - YVO4 (download all files)
    • Input .csv: Cavalli (2002) - fexp
    • Output files: Cavalli (2002) - JO , Cavalli (2002) - Combinatorial JO , Cavalli (2002) - Transitions
    • Notes: Eight combined transitions (more absorption bands are in overlap within each other), Input: fexp, provided constant refractive index (n=2.02) for all transitions. For calculation of transition probabilities, the value of refractive index is defined via Sellmeier formula, where A=n2 (A=4.0804). Output: Calculated JO parameters, Combinatorial JO analysis (163 possible combinations of absorption bands) and transition probabilities.
     
    2) Kaminskii (2002) - alpha-KGd(WO4)2 (download all files)
    Blank template: Eu template

    Blank template: Gd template

    Blank template: Ho template

    Reference files:  
    1) Walsh (1998) - LiYF4(download all files)
    2) Walsh (2006) - Y3Al5O12 (YAG)(download all files)
    Blank template: Nd template

    Reference files:  
    1) Walsh (2002) - Y2O3(download all files)
    Blank template: Pm template

    Reference files:  
    1) Shinn (1988) - 65PbO-20P2O5-6 In2O3 (PIP) glass (download all files)
    • Input .csv: Shinn (1988) sexp
    • Output files: Shinn (1988) JO , Shinn (1988) Combinatorial JO , Shinn (1988) Transitions
    • Notes: Seven combined transitions (more absorption bands are in overlap within each other), Input: Sexp, provided constant refractive index (n=1.76) for all transitions. For calculation of transition probabilities, the value of refractive index is defined via Sellmeier formula, where A=n2 (A=3.0976). Output: Calculated JO parameters, Combinatorial JO analysis (64 possible combinations of absorption bands) and estimated transition probabilities.
    Blank template: Pr template

    Reference files:  
    1) Merkle (2017) - RbPb2Cl5 (download all files)
    Blank template: Sm template

    Reference files:  
    1) Manjunath (2018) - Sr2SiO4 (download all files)
    2) Budchicha (2023) - TeO2BiCl3 glass (download all files)
      • Input .csv: Budchicha (2023) - fexp
      • Output files: Budchicha (2023) JO , Budchicha (2023) Combinatorial JO
      • Notes: Seven combined transitions (more absorption bands are in overlap within each other), Input: fexp values accompanied by provided constant refractive index (n=1.76) for all transitions. For calculation of Sexp and transition probabilities, the value of refractive index is defined via Sellmeier formula, where A=n2 (A=3.0976), Output: JO parameters, combinatorial JO analysis
    Blank template: Tb template

    Reference files:  
    1) Vasyliev (2013) - LiTbF4 (download all files)
    Blank template: Tm template

    Reference files:  
    1) Walsh (2006) - Germanate glass (download all files) 2) Bonner (2006) - Sr5(PO4)3F (S-FAP) (download all files)
      • Input .csv: Bonner (2006) - fexp
      • Output files: Bonner (2006) JO
      • Notes: Four combined transitions (more absorption bands are in overlap within each other), Input: linestrength values, Output: JO parameters, refractive index not included in the input file

     

    7. References

    1. Judd, B. Optical absorption intensities of rare-earth ions. Phys. Rev. 127, 750–761, 10.1103/PhysRev.127.750 (1962).

    2. Ofelt, G. Intensities of Crystal Spectra of Rare-Earth Ions. The J. Chem. Phys. 37, 511–520, https://doi.org/10.1063/1.466
    1701366 (1962).

    3. Vleck, J. The puzzle of rare-earth spectra in solids. J. Phys. Chem. 41, 67–80, 10.1021/j150379a006 (1937).

    4. Broer, L., Gorter, C. & Hoogschagen, J. On the intensities and the multipole character in the spectra of the rare earth ions.491
    Physica 11, 231–250, 10.1016/S0031-8914(45)80009-5 (1945).

    5. Walsh, B. Judd-Ofelt theory: principles and practices. Di Bartolo, B., Forte, O. (eds) Adv. Spectrosc. for Lasers Sens.442
    https://doi.org/10.1007/1-4020-4789-4_21 (2006).

    6. Hehlen, M., Brik, M. & Kramer, K. 50th anniversary of the Judd–Ofelt theory: An experimentalist’s view of the formalism461
    and its application. J. Lumin. 136, 221–239, 10.1016/j.jlumin.2012.10.035 (2013).

    7. Hrabovsky, J. et al. (Preprint) Doping ability, spectroscopic characterization and combinatorial Judd-Ofelt analysis of493
    Er-doped TeO2ZnOBaO ternary tellurite glasses. ResearchGate 10.13140/RG.2.2.32721.54886/1 (2024).

    8. Hrabovsky, J. LOMS.cz: interactive online software for Classical and Combinatorial Judd-Ofelt analysis with integrated496
    database of Judd-Ofelt parameters. Figshare doplnit (2024)